Integreat`RK`
Integreat`RK`

RKAbsoluteMonotonicityRadius

RKAbsoluteMonotonicityRadius[rk]

computes the radius of absolute monotonicity, also known as the strong stability preserving (SSP) coefficient, of rk.

Details and Options

  • Consider an ODE where a forward Euler discretization satisfies the monotonicity condition 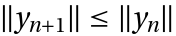for a convex functional 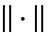with a step size restriction 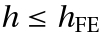. The radius of absolute monotonicity of a Runge–Kutta method is the largest positive constant 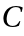such that the monotonicity condition holds for .
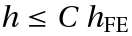  • The following options can be given:
  • EmbeddedFalsewhether to use the embedded coefficients
    StageNonetreat a stage as the solution
    DenseOutputFalsehow to evaluate dense output

Examples

open allclose all

Basic Examples  (2)

Get the radius of absolute monotonicity of the family of second order explicit Runge–Kutta methods:

Backward Euler is unconditionally strong stability preserving:

Options  (3)

Embedded  (1)

Get the radius of absolute monotonicity of an embedded method:

Stage  (1)

Get the radius of absolute monotonicity of a particular stage:

DenseOutput  (1)

Get the radius of absolute monotonicity for the dense output solution:

Tech Notes
▪
  • Runge–Kutta Methods