Integreat`RK`
Integreat`RK`

RKIStable

RKIStable[rk]

returns an algebraic condition equivalent to rk being stable on the imaginary axis.

Details and Options

  • A Runge–Kutta method is I-stable if 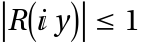for all y in TemplateBox[{}, Reals], where 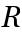is the linear stability function.
  • RKIStable returns True or False if rk does not contain free variables. Otherwise, it will return an (in)equality dependent on the free variables.
  • The following options can be given:
  • EmbeddedFalsewhether to use the embedded coefficients
    StageNonetreat a stage as the solution
    DenseOutputFalsehow to evaluate dense output

Examples

open allclose all

Basic Examples  (2)

Determine when two stage collocation methods are I-stable:

An explicit method cannot be I-stable:

Options  (3)

Embedded  (1)

Check I-stability for an embedded method:

Stage  (1)

Check I-stability for a particular stage:

DenseOutput  (1)

Check I-stability for the dense output solution:

Tech Notes
▪
  • Runge–Kutta Methods