Integreat`RK`
Integreat`RK`

RKErrorA

RKErrorA[rk]

computes the 2-norm of the principal error residuals of rk.

RKErrorA[rk,p]

computes the 2-norm of the order p residuals.

Details and Options

  • RKErrorA[rk,p] computes 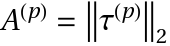, where 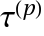is a vector of the order condition residuals of order .
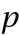  • The accuracy of Runge–Kutta methods of the same order can be compared with RKErrorA.
  • RKErrorA[rk] is equivalent to RKErrorA[rk,RKOrder[rk]+1].
  • The following options can be given:
  • EmbeddedFalsewhether to use the embedded coefficients
    StageNonetreat a stage as the solution
    DenseOutputFalsehow to evaluate dense output

Examples

open allclose all

Basic Examples  (1)

Compute of the classical fourth order Runge–Kutta method:

Compute through as well:

Options  (3)

Embedded  (1)

Compute for an embedded method:

Stage  (1)

Compute for a particular stage:

DenseOutput  (1)

Compute for the dense output solution:

Applications  (2)

Derive an optimal, two stage, explicit Runge–Kutta method:

Compare the accuracy of extrapolation methods with different step sequences:

Properties & Relations  (1)

RKErrorA is the 2-norm of the residuals from RKOrderConditions:

Tech Notes
▪
  • Runge–Kutta Methods