Integreat`RK`
Integreat`RK`

RKOrderConditions

RKOrderConditions[rk,p]

generates the order condition residuals of rk up to order p grouped by order.

RKOrderConditions[rk,{p}]

generates a list of p-th order residuals of rk.

Details and Options

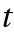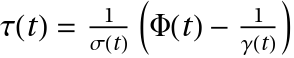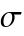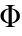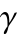  • Tree-based order condition theory is used to compute order condition residuals. For a rooted tree , the associated residual is , where , , and are the symmetry, elementary weight, and density of 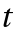, respectively.
  • RKOrderConditions[rk,p] generates a list of length p.
  • RKOrderConditions assumes rk satisfies the row simplifying assumption .
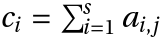  • The following options can be given:
  • EmbeddedFalsewhether to use the embedded coefficients
    StageNonetreat a stage as the solution
    DenseOutputFalsehow to evaluate dense output

Examples

open allclose all

Basic Examples  (2)

Check the order condition residuals of the classical fourth order Runge–Kutta method up to order five:

Generate third order conditions for a generic, two stage method:

Options  (3)

Embedded  (1)

Check the order condition residuals for an embedded method:

Stage  (1)

Determine how closely matches for the classical fourth order Runge–Kutta method:

DenseOutput  (1)

Check the order condition residuals for the dense output solution:

Applications  (2)

Solve for the family of explicit, three stage, third order Runge–Kutta methods:

Add a second order embedded method:

The classical fourth order Runge–Kutta method does not include dense output:

But third order dense output can be added:

Tech Notes
▪
  • Runge–Kutta Methods